Understanding SCE Thermal Noise Charts
A key feature of Signal Chain Explorer (SCE) is its built-in ability to calculate and display the thermal noise in your signal chain. In this article, we take a look at thermal noise and how it is modeled and displayed in SCE.
Thermal noise, aka Johnson or Nyquist noise comes about via random electron fluctuations which increase with the ambient temperature of your circuit components. All resistors exhibit this noise, which is Gaussian in nature, and this noise is deemed white, meaning it is present at all frequencies. Thermal noise is modeled in SCE by introducing an RMS error voltage associated with each resistor in the signal chain. For example, consider a simple resistive voltage divider, as shown below:
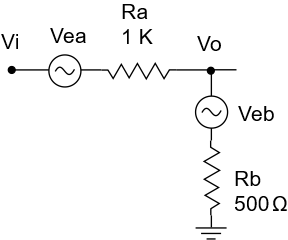
For each resistor, we add an error voltage in series with that resistor. Here, there are two error voltages Vea and Veb, which correspond to the resistors Ra and Rb, respectively. These error voltages can be calculated using the following well-known formula:
\(\displaystyle {{V}_{{noise}}}=\sqrt{{4KTBR}}\ {{V}_{{rms}}}\)
where K is Boltman’s constant, equal roughly to \(\displaystyle 1.38\times {{10}^{{-23}}}\), T is the ambient temperature in degrees Kelvin, often specified as 290 degK in most back-of-the-envelope calculations (and the default in SCE), B is the bandwidth of interest, in Hz, and R is the resistance in Ohms. Note that the resulting error voltage is Gaussian in nature, and we represent it as having units of Vrms.
Often, the thermal error voltage is specified in terms of a 1 Hz bandwidth, and the result is called the noise voltage density, with units \(\displaystyle {{V}_{{rms}}}/\sqrt{{Hz}}\). The noise density formula is:
\(\displaystyle {{V}_{{noise\ density}}}=\sqrt{{4KTR}}\)
The actual bandwidth is accounted for later by multiplying the noise density by the square root of that bandwidth:
\(\displaystyle {{V}_{{noise}}}={{V}_{{noise\ density}}}\times \sqrt{B}\)
Suppose our two resistances are 1000 Ohms and 500 Ohms, respectively. Then their thermal noise densities at a room temperature of 290 degK can be computed as:
\(\displaystyle Ve{{a}_{{noise\ density}}}=\sqrt{{4\times 1.38\times {{{10}}^{{-23}}}\times 290\times 1000}}=4\ nV/\sqrt{{Hz}}\)
and
\(\displaystyle Ve{{b}_{{noise\ density}}}=\sqrt{{4\times 1.38\times {{{10}}^{{-23}}}\times 290\times 500}}=2.83\ nV/\sqrt{{Hz}}\)
By the way, the 1000 Ohm resistor thermal noise calculation leads to a useful rule of thumb to remember when calculating thermal noise in your head:
\(\displaystyle 1000\ Ohms\Rightarrow 4\ nV/\sqrt{{Hz}}\)
Another useful rule of thumb:
\(\displaystyle 50\ Ohms\Rightarrow 1\ nV/\sqrt{{Hz}}\)
In order to incorporate thermal noise into SNR calculations, we must refer the noises to output. For our simple voltage dividers, the two error voltages referred to output using the voltage divider ratio:
\(\displaystyle Ve{{a}_{{rto}}}=Vea\times Rb/(Ra+Rb)=Vea\times 500/(1000+500)=Vea\times 0.3333\)
\(\displaystyle Ve{{b}_{{rto}}}=Vea\times Ra/(Ra+Rb)=Veb\times 1000/(1000+500)=Veb\times 0.6666\)
Now we can compute the thermal noise voltage densities of each resistor, referred to output, by using the numbers for the Vea and Veb noise densities calculated earlier:
\(\displaystyle Ve{{a}_{{rto\ density}}}=4\,nV/\sqrt{{Hz}}\times 0.3333=1.3333\ nV/\sqrt{{Hz}}\)
\(\displaystyle Ve{{b}_{{rto\ density}}}=2.83\,nV/\sqrt{{Hz}}\times 0.6666=1.8867\ nV/\sqrt{{Hz}}\)
SCE takes noise density calculations such as these and “sweeps” across the frequencies of interest in your simulation to produce a thermal noise chart. The figure below shows a (purposely coarse) thermal noise chart for our voltage divider example:
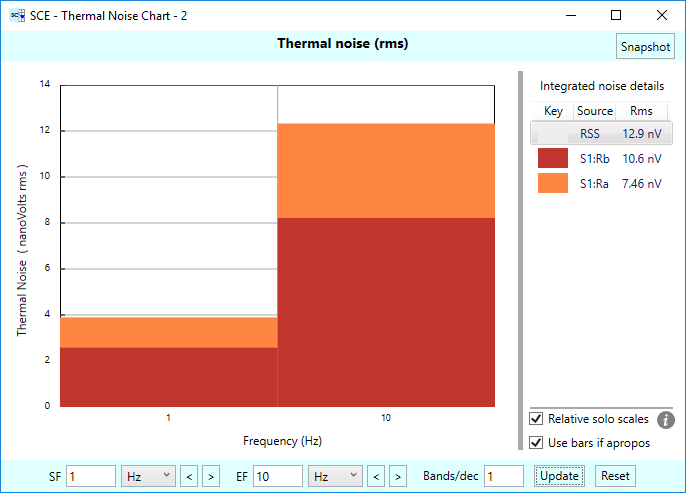
In this example, we are inspecting the thermal noise in the range of 1 Hz to 10 Hz. In computing thermal noise, SCE splits the specified frequency range into a series of bands, where each band is a chunk of the frequency spectrum. In our example here, we have two bands, one centered at 1 Hz, the other centered at 10 Hz. SCE computes the bandwidth of each band when computing thermal noise, and these bandwidths increase logarithmically with respect to the center frequency of the band. That’s because the thermal noise chart is logarithmic in nature. And it should be pointed out that each center point frequency is centered logarithmically in the band. To see this, below we’ve annotated the thermal noise chart to show the actual frequencies covered in each band of our example:
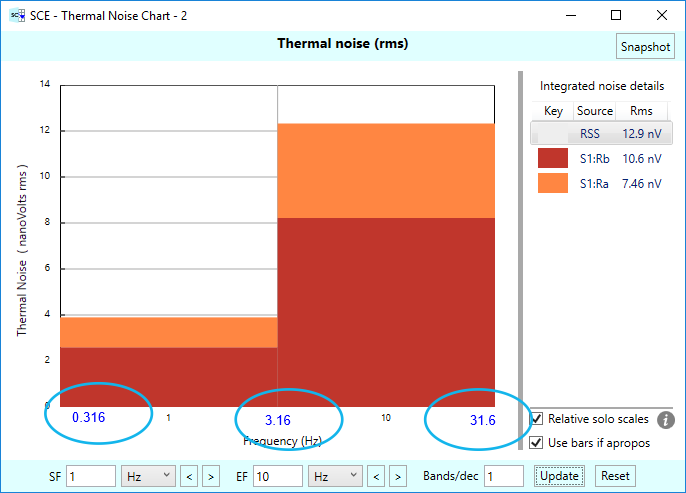
In our thermal noise chart, we’ve chosen a chart resolution of 1 band per decade. So we have a band centered at 1 Hz, the other at 10 Hz. If we chose a wider frequency range, say to 100 Hz, we’d see a band centered at 100 Hz, and so on. Also, we usually use a much higher resolution than one band per decade. The default is 20, and it’s not uncommon to choose a 100 bands per decade, or higher.
In our example, the first band, centered at 1 Hz, covers the frequencies from 0.316 Hz to 3.16 Hz. The second band, centered at 10 Hz, covers the frequencies from 3.16 Hz to 31.6 Hz. Note that the blue labels shown circled with ovals above do not normally appear on the thermal noise charts — only the center frequencies are labeled for real. We’ve shown the band edge frequencies here to help you see the range the bands really cover. Yes, this a bit confusing, and we here at RCD are currently re-evaluating this design choice. But do note that normally you use a much finer resolution in the charts, so the actual bandwidths are a lot smaller and this detail becomes less important, and if we included the band edge frequencies, the labels would in general become too cluttered.
Okay, let’s put our knowledge of the band frequencies to use. Our first band covers the frequencies 0.316 Hz to 3.16 Hz, so its bandwidth is 3.16-0.316 = 2.844 Hz. We can use this width, along with the computed noise densities, to compute the actual noise voltages, referred to output. So,
\(\displaystyle Ve{{a}_{{rto\ first\ band}}}=1.3333\ nV/\sqrt{{Hz}}\times \sqrt{{2.844\ Hz}}=2.248\ {{nV}_{{rms}}}\)
\(\displaystyle Ve{{b}_{{rto\ first\ band}}}=1.8867\ nV/\sqrt{{Hz}}\times \sqrt{{2.844\ Hz}}=3.182\ {{nV}_{{rms}}}\)
Note that these voltages are RMS voltages and are Gaussian in nature, as we stated earlier. You’ll soon see this fact come into play when computing total noise.
Okay, what about the second band? Well, its range is from 3.16 Hz to 31.6 Hz, so it’s bandwidth is 28.44 Hz. Note that it’s ten times the size of the first band, and so, we should see a corresponding increase in thermal noise — by a factor of a \(\displaystyle \sqrt{{10}}=0.316\), as a matter of fact. So,
\(\displaystyle Ve{{a}_{{rto\ second\ band}}}=1.3333\ nV/\sqrt{{Hz}}\times \sqrt{{28.44\ Hz}}=7.109\ {{nV}_{{rms}}}\)
\(\displaystyle Ve{{b}_{{rto\ second\ band}}}=1.8867\ nV/\sqrt{{Hz}}\times \sqrt{{28.44\ Hz}}=10.06\ {{nV}_{{rms}}}\)
The right side of the thermal chart gives a legend showing each noise source (in our case, the two resistors), along with the overall noise contribution of that choice.
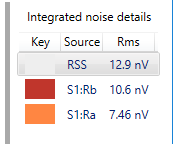
For example, the label “S1:Rb” stands for “resistor Rb of Stage #1, and we show an overall noise value for that resistor as 10.6 nVrms. The label “S1:Ra” stands for “resistor Ra of Stage #1”, and we shown an overall noise for that resistor as 7.46 nVrms. At the top of the legend we show the overall noise of the system, labeled as “RSS” (which stands for Root-Sum-Square) given as 12.9 nVrms. So how do these numbers correlate to what we just calculated? Next, we’ll take a look at how that’s done. And by the way, you are probably wondering about the different colors in the chart — and the heights of the bars. These will be explained in due course.
Let’s see how the overall noise (that is, over all the frequencies of interest) for Rb is computed. The way thermal noise works, being Gaussian and all, is that if you want to compute total noise, you take each individual rms value, square it, add the squares together, and then take the square root of the result. This is called the root-sum-square method. So the formula for Rb’s overall contribution of noise is
\(\displaystyle Ve{{b}_{{overall}}}=\sqrt{{Ve{{b}_{{band1}}}^{2}+Ve{{b}_{{band2}}}^{2}}}=\sqrt{{{{{3.182}}^{2}}+{{{10.06}}^{2}}}}=10.55\ {{nV}_{{rms}}}\)
We’ve rounded this to 10.6 nV in the chart legend.
Likewise, for Ra, we have:
\(\displaystyle Ve{{a}_{{overall}}}=\sqrt{{Ve{{a}_{{band1}}}^{2}+Ve{{a}_{{band2}}}^{2}}}=\sqrt{{{{{2.248}}^{2}}+{{{7.109}}^{2}}}}=7.4556\ {{nV}_{{rms}}}\)
which we’ve rounded to 7.46 nV in the chart legend.
Okay, what about total noise in the system? Well, we do the same root-sum-square trick — just at a higher level. We square each noise source’s contribution, add the squares together, and take the square root of the result:
\(\displaystyle Tnois{{e}_{{overall}}}=\sqrt{{Ve{{a}_{{overall}}}^{2}+Ve{{b}_{{overall}}}^{2}}}=\sqrt{{{{{7.4556}}^{2}}+{{{10.55}}^{2}}}}=12.92\ {{nV}_{{rms}}}\)
which we’ve rounded to 12.9 nV in the chart legend.
There’s a lot of root-sum-squaring going on when thermal noise calculations are involved. Thankfully, SCE does all this tedious work for us.
Next, we take a look at the bars in the chart itself, and show how to interpret the heights and colors of the bars. Let’s look at the first band to get things started:
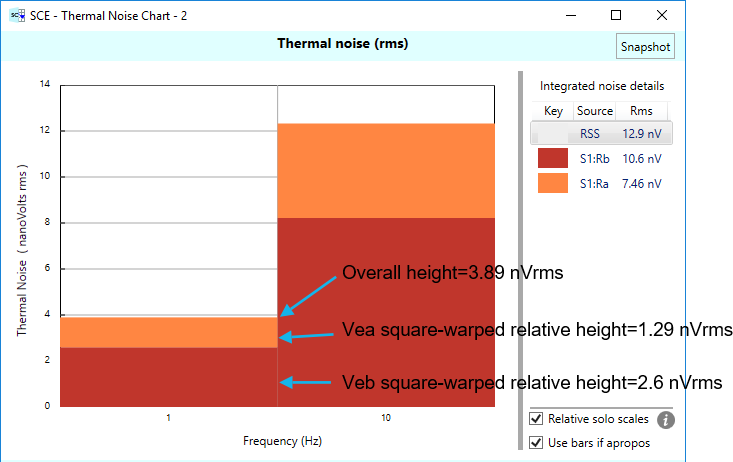
The first thing to note is that each band is composed of different colored rectangular bars stacked vertically. The bar colors correspond to those given in the chart legend. In this case, the red color is for Veb, the thermal noise due to resistor Rb. The orange color is for Vea, the thermal noise due to Ra. The noise contributions of the various sources are sorted such the that source with the most overall contribution (over all the bands) is drawn first, on the bottom. The source with the second most overall contribution has it’s contribution rectangle stacked on top of the first, and so on. The relative heights of these rectangles are such that, when added together, they represent the overall thermal noise for that given band. Next, we explain in detail how these heights are computed.
First, the overall noise contribution for the first band: In our example, we have the two values we calculated earlier:
\(\displaystyle Ve{{a}_{{rto\ first\ band}}}=1.3333\ nV/\sqrt{{Hz}}\times \sqrt{{2.844\ Hz}}=2.248\ {{nV}_{{rms}}}\)
\(\displaystyle Ve{{b}_{{rto\ first\ band}}}=1.8867\ nV/\sqrt{{Hz}}\times \sqrt{{2.844\ Hz}}=3.182\ {{nV}_{{rms}}}\)
If you add these up using root-sum-square, (remember, these are Gaussian values represented in RMS form) you end up with the overall noise contribution for the logarithmic band centered at 1 Hz:
\(\displaystyle {{V}_{{noise\ first\,band}}}=\sqrt{{{{{2.248}}^{2}}+{{{3.182}}^{2}}}}=3.896\ {{nV}_{{rms}}}\)
What about the relative heights of the colored bars? We’d like to graphically display how much each source contributes to the overall noise, relative to the others. There are many different mappings that could be used — a linear mapping, for example. But note how the noise contributions are squared before summing. Due to this squaring, the higher the noise source’s contribution, the more it will tend to dominate the overall result. The relative proportion is, for sure, not linear. SCE accounts for this by using a “square-warping” when determining relative heights:
\(\displaystyle RelativeNois{{e}_{i}}=(Nois{{e}_{i}}^{2}/Overal{{l}_{{noise}}}^{2})\times Overal{{l}_{{noise}}}\)
Take noise source Ra, for example. It’s relative noise contribution for the first band can be computed (using the overall noise for the first band that we computed earlier) as:
\(\displaystyle RelativeNois{{e}_{{Ra\ first\ band}}}=({{2.248}^{2}}/{{3.896}^{2}})\times 3.896=1.297\,n{{V}_{{rms}}}\)
Likewise for Rb:
\(\displaystyle RelativeNois{{e}_{{Rb\ first\ band}}}=({{3.182}^{2}}/{{3.896}^{2}})\times 3.896=2.6\,n{{V}_{{rms}}}\)
If you add these relative heights together, you’ll get back to overall noise contribution for the first band. (Well, there is some round-off error due to how we’ve presented the calculations here:)
\(\displaystyle {{V}_{{noise\ first\ band}}}=1.297+2.6=3.897\ n{{V}_{{rms}}}\)
To recap: We’ve arranged the relative heights of the noise contributions so that they reflect the square-domination of the bigger noise sources, but in such a way that when the stacked heights are added together, the result accurately reflects the overall noise for the given band.
Let’s now do the same for the second band. Here’s the graph annotated:
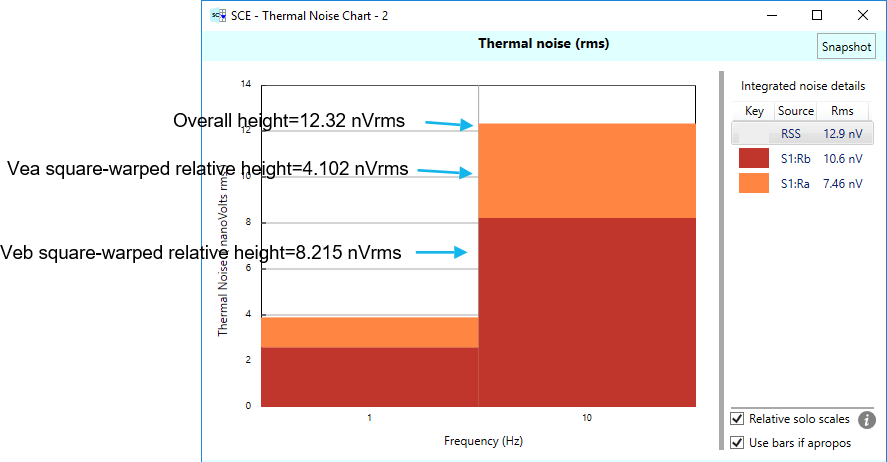
First the individual source contributions:
\(\displaystyle Ve{{a}_{{rto\ second\ band}}}=1.3333\ nV/\sqrt{{Hz}}\times \sqrt{{28.44\ Hz}}=7.109\ {{nV}_{{rms}}}\)
\(\displaystyle Ve{{b}_{{rto\ second\ band}}}=1.8867\ nV/\sqrt{{Hz}}\times \sqrt{{28.44\ Hz}}=10.06\ {{nV}_{{rms}}}\)
Computing the overall contribution for band 2:
\(\displaystyle {{V}_{{noise\ second\,band}}}=\sqrt{{{{{7.109}}^{2}}+{{{10.06}}^{2}}}}=12.32\ n{{V}_{{rms}}}\)
Next, the relative contributions:
\(\displaystyle \begin{array}{l}RelativeNois{{e}_{{Ra\ second\ band}}}=({{7.109}^{2}}/{{12.32}^{2}})\times 12.32=4.102\,n{{V}_{{rms}}}\\RelativeNois{{e}_{{Rb\ second\ band}}}=({{10.06}^{2}}/{{12.32}^{2}})\times 12.32=8.215\,n{{V}_{{rms}}}\end{array}\)
These add up to the original band 2 overall noise:
\(\displaystyle {{V}_{{noise\ second\ band}}}=4.102+8.215=12.32\ n{{V}_{{rms}}}\)
To double check our results, let’s root-sum-square (RSS) the heights of the two bands, and see if we get back the overall noise in the system of 12.92 nVrms:
\(\displaystyle \sqrt{{{{{3.986}}^{{2+}}}{{{12.32}}^{2}}}}=12.92\ n{{V}_{{rms}}}\)
Before, we calculated the overall noise by RSS’ing the individual noise source contributions. Here, we’ve calculated the overall noise by RSS’ing each band’s contributions. The end result is the same.
We’ve had a colleague say to us that SCE is “just a giant spreadsheet.” Well, that’s true in a sense. And the above calculations show how the thermal noise calculations have a spreadsheet/matrix-like feel to them. Just be glad you don’t have to implement this spreadsheet yourself — especially as your circuits get more complex than a simple voltage divider. The computations for thermal noise referred to output in arbitrary circuit configurations get rather complicated in a hurry. Be glad that SCE is on your side, doing these calculations for you, automatically.
Okay, so far we’ve used a very coarse resolution for our thermal noise charts. Next, we’re going to increase that resolution and see how that affects the look and feel of the charts. First, we’ll go from 1 band per decade to … two bands per decade. Yes, we’re feeling rather adventurous! Here’s the resulting chart:
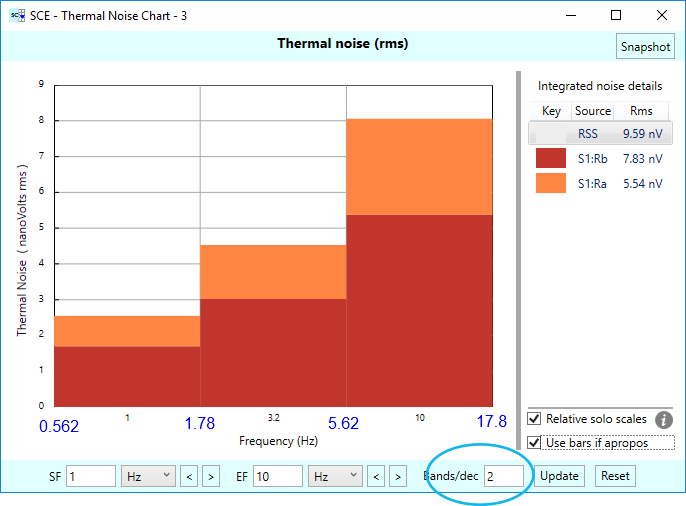
We denoted the start and end frequencies of each band using blue labels, and as before, these labels don’t actually appear on the real chart. We just show them here to help in understanding how the bands work. The main upshot is to notice that the bands are smaller in frequency width than before, and that this means the “spill over” at the ends of the 1 – 10 Hz frequency range is smaller. These two facts mean that: (a) The heights of each band are going to be shorter, since there is less bandwidth to cover, and (b) the overall noise is going to be less than we got before — in this case, 9.59 nVrms, instead of 12.92 nVrms. Note that the chart above, with more resolution, is the more accurate one. And as you might expect, if you increase the resolution (bands per decade) even further, you’ll get even more accurate results.
So far, we’ve drawn the charts using rectangular bars. That’s because we’ve checked the box that says “Use bars if apropos” at the bottom of the legend. (This box is checked by default.) With this box checked, SCE will plot using rectangular bars as long as the number of rectangles produced isn’t too large. Once a certain threshold is reached, SCE reverts to drawing polygon curves. Next, we’ll see that in action, but we’ll force the polygon curves by turning off the “Use bars if apropos” checkbox, leaving all other parameters alone. We end up with the following chart:
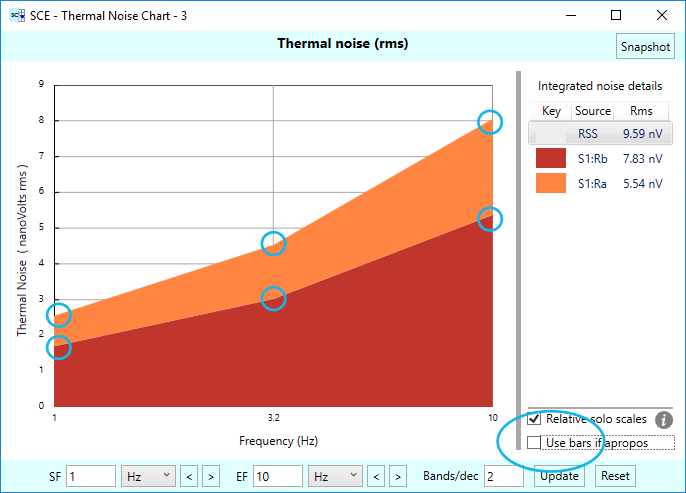
We’ve annotated this chart with blue circles and ovals to indicate key features of the changes made. As before, these annotations don’t appear on the real chart.
Instead of drawing rectangular bars with the bar centers aligned with the center point frequencies of our bands, instead, we draw polygon curves, with the Y-value of each point of the polygons corresponding to the height for a given band, and the X-axis location is at a corresponding center point frequency. Also, notice the subtle shift in the X-axis labels, to accommodate this shift in how the points are drawn. (Compare with the previous “bar chart”.) The graph starts and ends at 1 Hz and 10 Hz, instead of before and after these frequencies.
Alrighty then, let’s get even more adventurous and move on out to … 20 bands per decade! Woohoo! Here is the resulting chart:
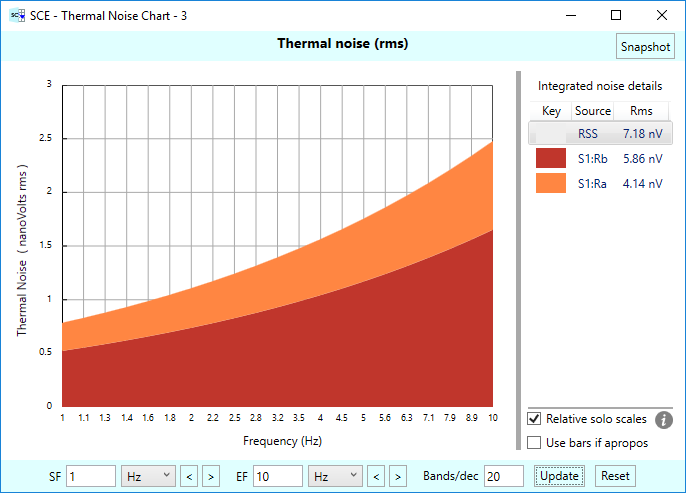
Note how our polygon curves are getting smoother. But do note: The results can be misleading, since the only data points that are known for sure are at the center point frequencies. In-between those frequencies? We don’t really know. There might be a spike, for instance, that gets completely missed. So sometimes it behooves you to experiment with higher resolution to see if you’ve missed anything.
With the smaller bandwidths, the resulting overall noise calculations are getting more accurate. Now how the chart is saying 7.18 nVrms total noise, instead of the 12.92 nVrms we originally got for one band per decade, and the 9.59 nVrms we got for two bands per decade.
It’s been our experience that, in general, 20 bands per decade gives you reasonably accurate results — unless your circuit’s response has resonances that can spike. In cases like that, you might want to try 100 bands per decade, or even higher, to try and capture those spikes.
So far, we’ve kept our frequency range covering 1 to 10 Hz. The overall noise computed in the chart is based solely on that frequency range, but as we mentioned earlier, thermal noise is white, and as such, covers all frequencies. What happens if we cover more in our chart? Let’s see what happens if we extend our frequency range out to 100 Hz. To do this, the easy way is to use the frequency range extension buttons on the right side, which manipulate the ending frequency. (There are corresponding buttons for the starting frequency on the right side). Each click on the outward right-arrow button extends the frequency by a decade, as shown below:
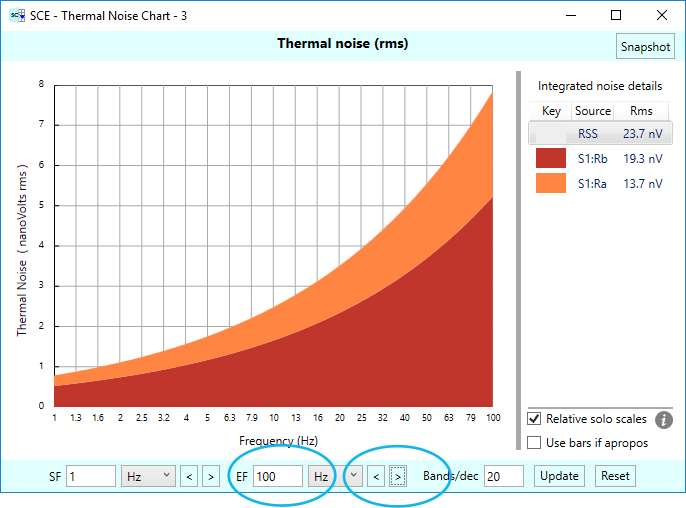
Notice how the noise is rising at the higher frequencies. Our total noise is up too, from 7.18 nVrms to 23.7 nVrms. What gives? Two things: (1) Remember, thermal noise is white, covering all frequencies, (2) At the higher frequencies, the bandwidth of each band is wider too — in a logarithmic fashion. A wider bandwidth means more noise in that band. The end effect is the noise appears to be rising exponentially in the chart. It isn’t really, it’s just that appears that way as the bands get wider and wider. What’s really happening is that the white noise, if plotted on a linear chart, would be a straight line. But since our thermal charts are logarithmic in nature, those straight lines get morphed into exponentially rising curves by the increasingly wider bands.
We’ve thought long and hard about this rising noise phenomenon, and whether the charts should be shown linearly instead of logarithmically — the root cause. There is no easy answer, but we deem the current logarithmic method better than all the alternatives, and besides, we reason that having the noise appear to be rising is a good thing — it may make the user panic just enough to realize that noise is occurring at high frequencies, and that it needs to be addressed. You should duly note that if you have an A/D converter in your signal chain, it samples that noise, regardless of frequency. This unfiltered high frequency noise can be a real problem. It can get intermodulated down into frequency ranges you’d rather it not.
Continuing on with extending the frequency range, we dip our toes deeper into the water and go out to 10 KHz by clicking the right side frequency range extender button a few times:
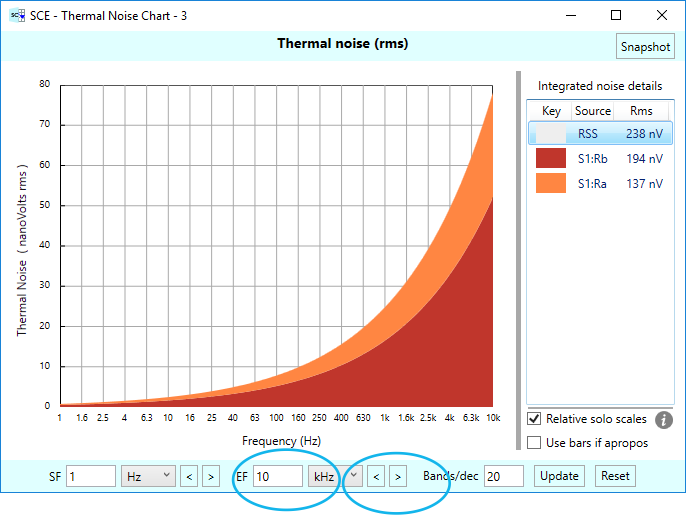
Now our total thermal noise is up to 238 nVrms. For our simple voltage divider circuit, which can’t filter out any high frequency thermal noise, this rising trend will continue — out to the THz range anyway. When the THz range is encountered, quantum effects kick in, as noted by Nyquist, and the thermal noise will start dropping off, all on its own. We’ll leave the demonstration of this effect for another blog post.
Next, we want to illustrate some of the other features of the thermal charts in SCE. In particular, we can isolate the thermal noise for a single noise source, and see it on it’s own. We do this by clicking on the appropriate noise source entry in the chart legend. For example, here is the result for S1:Rb:
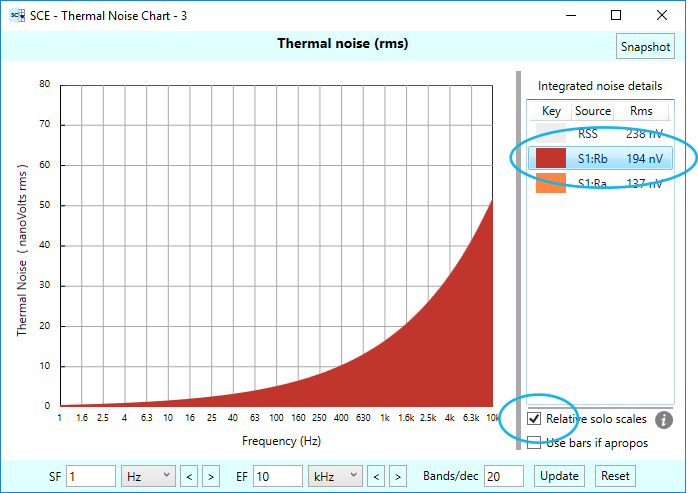
Soloing a noise source this way produces a plot with a single curve — in this case for noise from resistor Rb. The scale of the plot is “relative” — relative to the overall noise. This is accomplished by checking the “Relative solo scales” check box (which defaults to checked.) Notice the scale of the chart is the same as it was with the two noise sources combined, shown in the previous chart.
NOTE: If you want to go back to displaying all the noise sources, click the “RSS” label at the top of the legend.
Let’s see what happens when we solo the Ra noise:
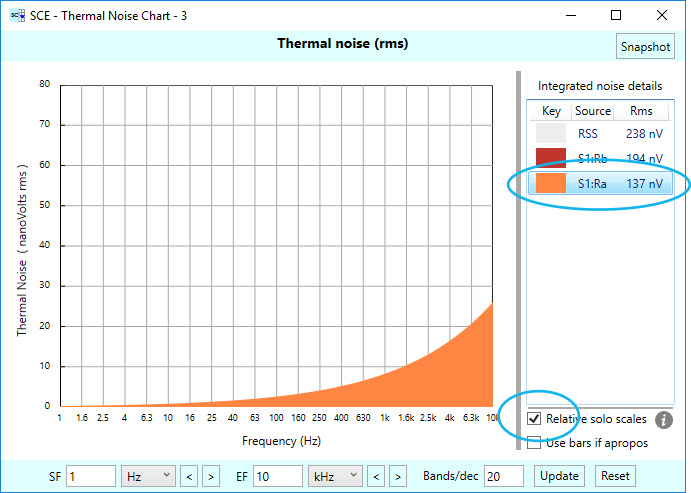
In case you are wondering about the max height of the noise in the chart (roughly 25 nVrms, occurring at 10 kHz) and how that corresponds to the value in the legend (137 nVrms): Remember, the legend is showing total RMS noise over all frequency bands for the noise source of interest. It’s in effect the integration of the area under the noise curve. (And the more bands per decade, the more accurate that integration.) But note this integration is accomplished via the root-sum-square of each band’s contribution.
Sometimes the relative size of the noise sources is dramatically different, and some noise sources may be small enough to not show up at all in the relative plots. In that case, you can uncheck the “Relative solo scales” check box, so that the noise is plotted to its own natural scale. Our voltage divider example doesn’t have this problem, but we’ll show you have to handle such cases anyway: You turn off the “Relative solo scales” checkbox. Here are our two noise sources plotted with the relative scale turned off. Notice how the Y-axis scale of the charts changes to accommodate the natural ranges of the two noises:
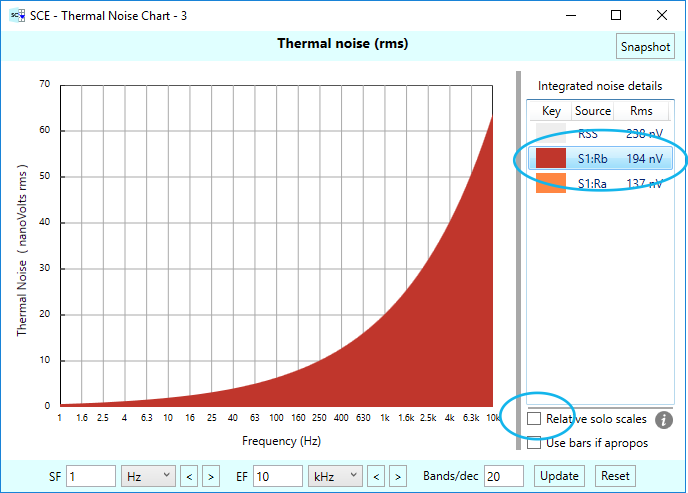
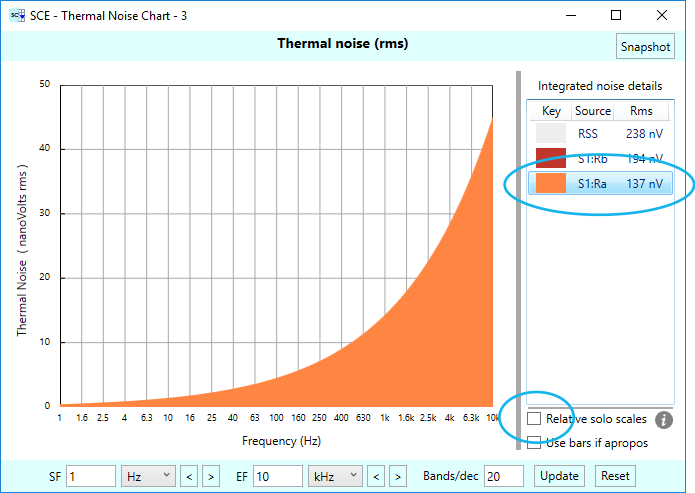
In this voltage divider example, the two solo thermal noise plots have the same shape — these are simple resistors after all. The only difference is in scale — that scale being determined by the referred-to-output voltage divider ratio.
Okay, we’ve covered most of the details of the thermal noise chart. We haven’t covered the Update and Reset buttons — or have we given a detailed description of how to use the frequency ranges at the bottom of the charts. We’ll cover these features in a subsequent blog post. But for now, we’d like to show a more interesting thermal noise chart, using a more complicated circuit.
In this more complex example, we have a non-inverting “gain follower” amplifier stage, with a RIAA equalization filter in the feedback path. This stage has multiple noise sources: the feedback path resistors, (there are three of them), a resistor shunting to ground, and another noise source we haven’t talked about: the amplifier itself.
Op-amps have resistances: In the transistor gateways, the compensation networks, current sources, and what have you. The actual configuration is of course, implementation dependent. These resistances, like all resistances, contribute thermal noise, and fortunately for us, op-amp manufacturers usually include a noise specification in their op-amp datasheet that covers all these noises and sums them up into a single number. For example, an NE5532 op-amp has around 5 nV/rootHz of thermal noise, according to the datasheet for this part.
We model the thermal noise of an op-amp by injecting an error voltage at one of the input pins. For our non-inverting stage, we inject it at the positive pin. Here is the closed-loop amplifier stage in all its glory, with noise error voltages added for the amplifier and all the external resistors in the circuit:
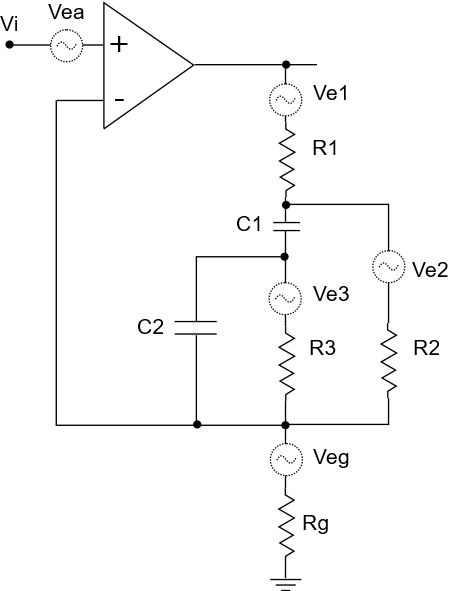
Here is the thermal noise chart for this circuit, using a NE5532 op-amp, and plotted from 1 Hz to 100 kHz, 20 bands per decade:
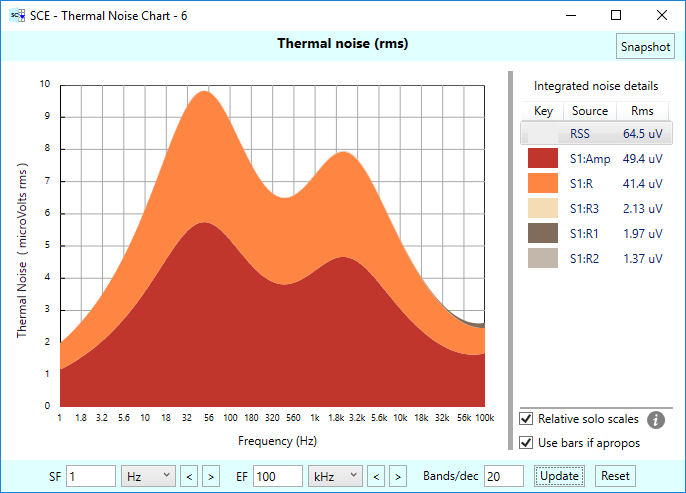
From this chart, we see that the amplifier itself contributes the most noise, followed closely behind by the resistor to ground (denoted as S1:R in the chart). The feedback resistors contribute much smaller amounts. One is barely visible in the stacked chart, the other two aren’t visible at all. You can experiment by soloing these noise sources to see their relative shapes, but since some of them have such small areas relative to the others, they won’t really show up. Fortunately, you can turn off the “Relative solo scales” checkbox, and see them self-scaled. We show all the noise sources plotted this way in the following figure. Do note that each plot has a different Y-Axis scale. Don’t be fooled!
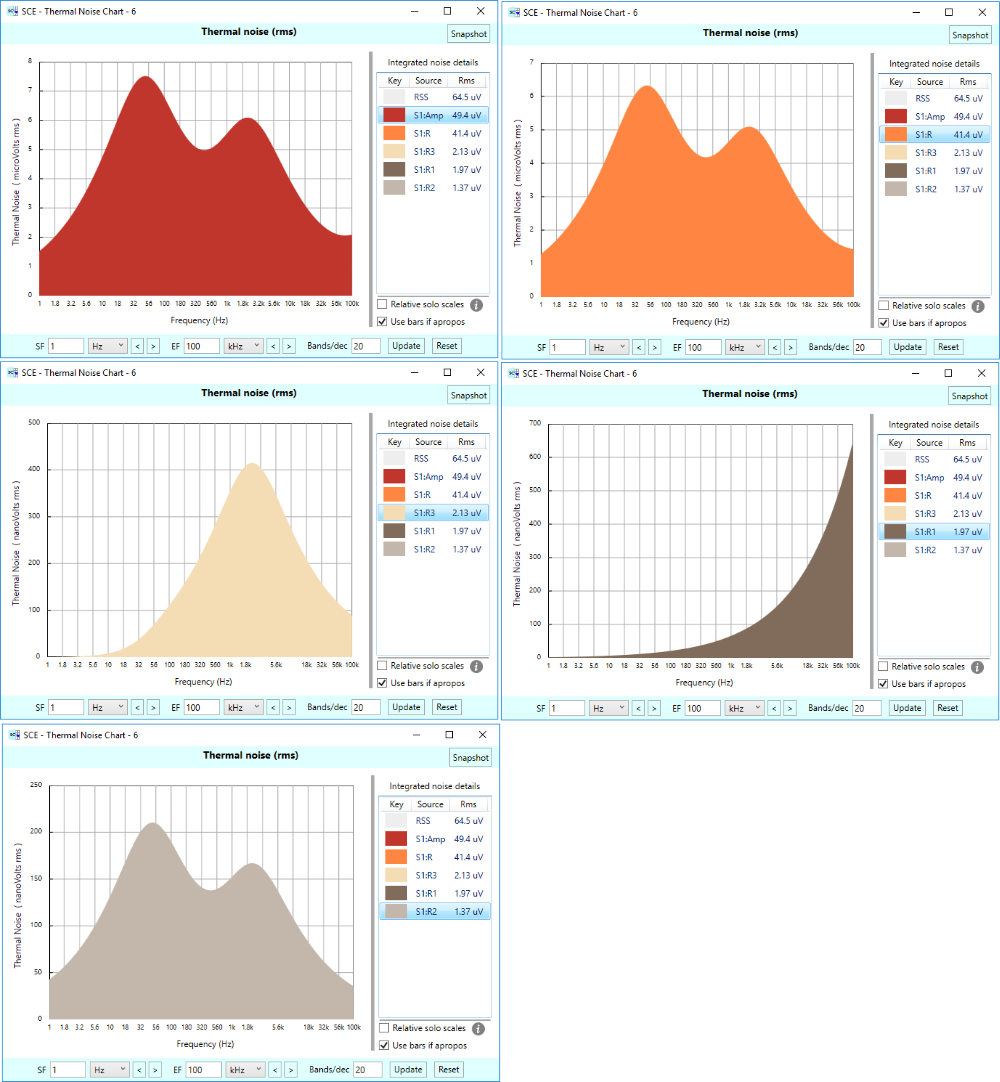
NOTE: If you experiment by clicking the “Relative solo scales” checkbox on and off for a soloed noise source, you might see the resulting plot not only change scale (and/or size), but it might change shape as well. What gives? Remember that with relative scaling, the noise for a single source is plotted relative to the other noise sources, using a square-warped mapping. Turning off relative scales gets rid of this warping. Also, a noise source’s “height” in the relative scales depends on what the other noise sources are doing, so if a noise source is large for a particular frequency band, but the other sources are not, that first noise source will take on a much larger height than it would otherwise, if plotted on its own without relative scaling.
As before, we are only showing a portion of the frequency range. You can experiment and see what happens out at higher frequencies. You might be surprised! (And we note that we’ll be covering the really high frequencies — such as a THz, in a subsequent blog post.)
Conclusion
You’ve now had a solid introduction on how to interpret the thermal noise charts in SCE. When I told a colleague how long this post was turning out to be, he asked, “How can such a post be that complicated, with just a simple voltage divider?” Well, it’s because even though SCE computes and plots thermal noise almost instantaneously with little effort on your part, there’s a lot going on under the hood. Just be thankful you don’t have to do this by hand!
One final thing to point out: In the last example involving an amplifier stage, we plotted all the solo noise contributions, and you got to instantaneously see their shapes, however small. That’s a lot of power at your fingertips, and we wonder if this type of clearly visualized behavior has really been seen before, with such ease.
If you’re lucky, thermal noise is often small, so small it may be hard to see in a real circuit with a scope. It’s in that class of sometimes-invisible phenomenon that we hope to make visible in SCE. Who knows, for example, what someone might uncover looking at the tiny shapes of the thermal noise in each of the resistors in an RIAA feedback network. Maybe you’ll be the one to uncover some great secret!
Bon voyage on your explorations! And good luck.
Comments
Understanding SCE Thermal Noise Charts — No Comments
HTML tags allowed in your comment: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>